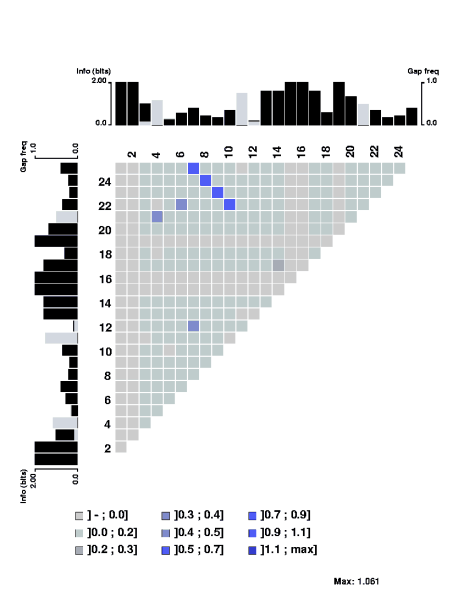
The mutual information content of a structural alignment (refound by foldalign of the following RNA sequences (sequences from Tuerk et al. PNAS 89, pp 6988-6992, 1992.):
|
CCAGAGGCCCAACUGGUAAACGGGC CCG-AAGCUCAACGGGAUAAUGAGC CCG-AAGCCGAACGGGAAAACCGGC CC-CAAGCGC-AGGGGAGAA-GCGC CCG-ACGCCA-ACGGGAGAA-UGGC CCGUUUUCAG-UCGGGAAAAACUGA CCGUUACUCC-UCGGGAUAAAGGAG CCGUAAGAGG-ACGGGAUAAACCUC CCG-UAGGAG-GCGGGAUAU-CUCC CCG--UGCCG-GCGGGAUAU-CGGC CCG-AACUCG-ACGGGAUAA-CGAG CCG--ACUCG--CGGGAUAA-CGAG |
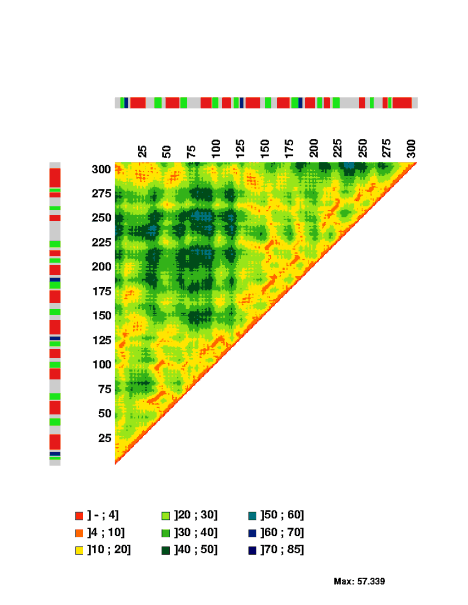
For sequences with a set of three-dimensional coordinates, for example PDB entry 1raa chain A, MatrixPlot generates the plot
Below it is discussed how to modify the graphical output of MatrixPlot. The graphical output is given in postscript files. Any submitted data is kept confidential and deleted a short time after submission.
Data Formats
- Inform formats:
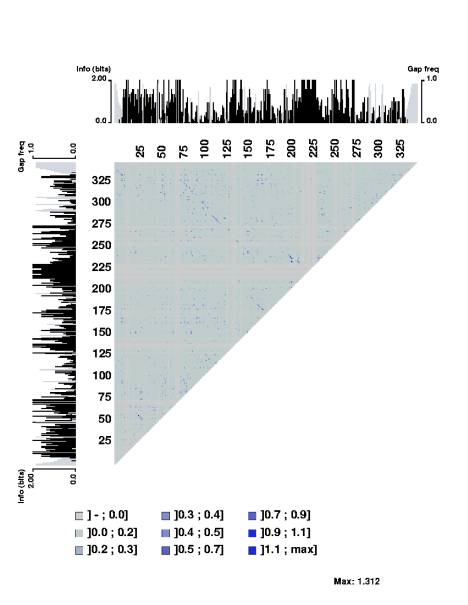
The formats for Inform are those that can be used for the MatrixPlot pages for generating mutual information plots of nucleotide sequence and proteins. The formats are a simple align format, fasta format and the msf format. Examples: - pdb2mp formats
- MatrixPlot format
Program Options (man pages)
The options to Inform, pdb2mp, MatrixPlot, and Zoom are described in the pages given below. Source code requests: send email to gorodkin@cbs.dtu.dk.
WWW Interface
The web interface of MatrixPlot consist of four pages, and has been made from the programs presented above: mutual information plots for RNA or DNA alignments, mutual information plots for protein alignments, distance matrices of sequences with a set of three-dimensional coordinates, and a page that takes a user produced mp file. Some of the command line options of the individual programs have been combined into one field on the corresponding web page. This is described here:-
Mutual information for nucleotide
sequence alignments
This page contains the options to Inform and all the relevant options of MatrixPlot to generate mutual information plots. -
Mutual information for protein sequence
alignments
This page contains the options to Inform ("complementarity matrix" is not defined) with mtype=1 (standard form of mutual information), and all the relevant options of MatrixPlot. -
Distance matrices
This page contains the options to pdb2mp, as well as the relevant MatrixPlot options to generate distance matrices of sequences with a set of 3D coordinates. The user may also enter the name of a PDB entry. If the chain identifier is omitted a distance matrix will be generated for the first identifier in the PDB entry. -
User matrix
This page allows the user to submit an mp file. All MatrixPlot options are available on that page.
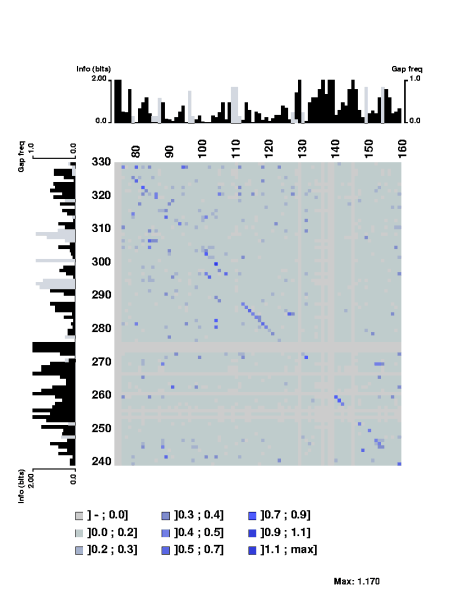
The stretch of covarying positions corresponds to the main stem of the RNA secondary structure. Note that the trace is interrupted by a few positions having complete sequence conservation. The respective parts of the sequence logo profile have also been displayed along the edges of the plot.
Export user data directly to MatrixPlot
The user data can automatically be exported to MatrixPlot thorugh the
web. This would typically be data generated from another web page which then
can be exported for graphical manipulation, such as zooming in on a region.
Only a single button is needed, as the form can be written using hidden
variables.
Discussion of Information Content
Two issues on information content for sequence/structure alignments are discussed here. First the contribution to the computation of information content when gaps are included in the alignment, and secondly the sample size robustness of mutual information for RNA secondary structure co-variance analysis. For background and details consult the mentioned references.
-
Calculating the information content of an alignment that have gaps.
The conceptual problem in computing the information content or relative entropy of an alignment that has gaps is the background probablities. The background probabilities are typically found by counting base (or amino acid) frequencies in the genomes (or data set) from which the aligned sequences originate. The gaps, however, do not appear before the alignment is made, so a ``gap background probability'' or a ``gap expectation value'' cannot be dealt with in the same way. It only makes sense to talk about this when the alignment has been performed.
Calculation of the information content of an alignment containing gaps has been derived by Hertz and Stormo, 1995 (In Lim & Cantor (eds), Proc. of the Third Int. Conf. on Bioinformatics and genome Res., pp. 201-216). They derived the expression
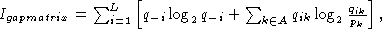
 and
and  are the fraction
of gaps and symbol k at position i in the alignment, and where
k is a symbol in the alphabet A. The fraction
are the fraction
of gaps and symbol k at position i in the alignment, and where
k is a symbol in the alphabet A. The fraction 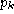 is the background probability of symbol
k, so
is the background probability of symbol
k, so 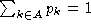 . Note that if
only a few sequences contain a gap (
. Note that if
only a few sequences contain a gap (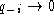 ) or almost all
sequences have a gap (
) or almost all
sequences have a gap (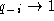 ) at some position
i, the ``gap'' term does not contribute to the sum. Since the gap
background probability is one in this expression, then all the background
probabilities sum to 2 rather than one, which is the formal claim to define
information content or relative entropy. This is resolved as follows. Hertz and
Stormo derived a large-devation rate function given by
) at some position
i, the ``gap'' term does not contribute to the sum. Since the gap
background probability is one in this expression, then all the background
probabilities sum to 2 rather than one, which is the formal claim to define
information content or relative entropy. This is resolved as follows. Hertz and
Stormo derived a large-devation rate function given by
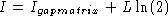
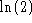 to the
information content on each of L positions in the alignment. Clearly,
the difference between I and
to the
information content on each of L positions in the alignment. Clearly,
the difference between I and 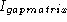 , is where to put
the baseline in a sequence logo profile plot. The normalizing factor of
Hertz and Stormo was found
by considering the minimum of
, is where to put
the baseline in a sequence logo profile plot. The normalizing factor of
Hertz and Stormo was found
by considering the minimum of 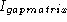 .
When using the normalizing factor, one interpretation is that the a
priori expectation to gaps is probability 0.5, however, another
interpretation is that one has two models, one for which the expectation values
for all the symbols sum to one, and one model dealing only with gaps and the
expectation to gaps is one. When combining the two models a (re-)normalization
of all the parameters can be introduced.
.
When using the normalizing factor, one interpretation is that the a
priori expectation to gaps is probability 0.5, however, another
interpretation is that one has two models, one for which the expectation values
for all the symbols sum to one, and one model dealing only with gaps and the
expectation to gaps is one. When combining the two models a (re-)normalization
of all the parameters can be introduced.
The considerations for any gap background probability can in general be extended by subtracting
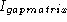 from the standard
form
from the standard
form
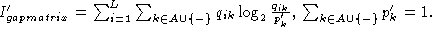
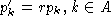 , it is easily
found that
, it is easily
found that 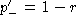 . Clearly
. Clearly 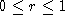 . Hence, the
normalizing factor and the a priori expectation of gap frequency is
directly related and the same when
. Hence, the
normalizing factor and the a priori expectation of gap frequency is
directly related and the same when 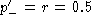 . Using this
relation one can readily write
. Using this
relation one can readily write
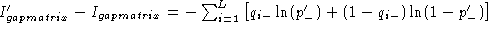
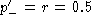 the difference is equal to
the difference is equal to 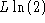 , and the same as above is obtained. The result
becomes independent of
, and the same as above is obtained. The result
becomes independent of 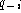 . The
interpretation of a gap a priori probability of 0.5 also makes sense.
If no prior knowledge is known about the alignment it makes sense to expect
gaps to appear randomly, i.e. having an a priori expectation of 0.5.
So a ``renormalization'' of the two sets of probabilities, the set of base
frequencies, and the gap probability, ensures that the background probabilities
sum to one and fulfill the formal claim to define information content.
. The
interpretation of a gap a priori probability of 0.5 also makes sense.
If no prior knowledge is known about the alignment it makes sense to expect
gaps to appear randomly, i.e. having an a priori expectation of 0.5.
So a ``renormalization'' of the two sets of probabilities, the set of base
frequencies, and the gap probability, ensures that the background probabilities
sum to one and fulfill the formal claim to define information content.
The current version of Inform computes the information content according to
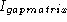 , but MatrixPlot contains an option ``neg'' for
which the baseline can be moved as described (when neg=n). Otherwise (when
neg=y) the baseline is placed so that ``negative information content'' can show
up on the profile. This can be useful in identifying positions which neither
contains many or few gaps, but really is degenerated.
, but MatrixPlot contains an option ``neg'' for
which the baseline can be moved as described (when neg=n). Otherwise (when
neg=y) the baseline is placed so that ``negative information content'' can show
up on the profile. This can be useful in identifying positions which neither
contains many or few gaps, but really is degenerated.
-
Mutual information only for basepairs
As has been discussed by Gorodkin et al. (Comput. Appl. Biosci., 13:583-586, 1997) and used in the display of structure logos the mutual information content for RNA sequences can be limited to include only pairs of bases that are complementary. In that way a more relevant measure is constructed. This is done by defining a complementary matrix (Gorodkin et al. Nucl. Acids. Res. 25:3724-3732,1997) which lists the bases that are complementary. The complementary matrix lists all bases against themselves, and a number is assigned to indicate the degree of ``belief'' in the complementarity. The matrix is clearly symmetric and most positions in the matrix hold the value zero. The mutual information between position i and j in the alignment using the complementary matrix is given by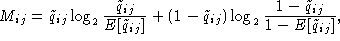
(A) 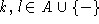 , A the alphabet, and where
, A the alphabet, and where 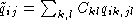 and
and 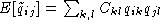 . The element
. The element 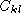 of the complementary matrix
lists the degree of complementarity between base k and l. The
fraction of pairs of base k at position i and base l at
position j is
of the complementary matrix
lists the degree of complementarity between base k and l. The
fraction of pairs of base k at position i and base l at
position j is 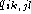 and
and 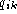 is the
fraction of base k at position i. Gaps is dealt with by having
is the
fraction of base k at position i. Gaps is dealt with by having
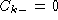 for any base k.
There are in particular two qualitative differences between this measure
and the standard form of mutual
information given by
for any base k.
There are in particular two qualitative differences between this measure
and the standard form of mutual
information given by
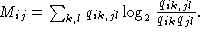
(B) 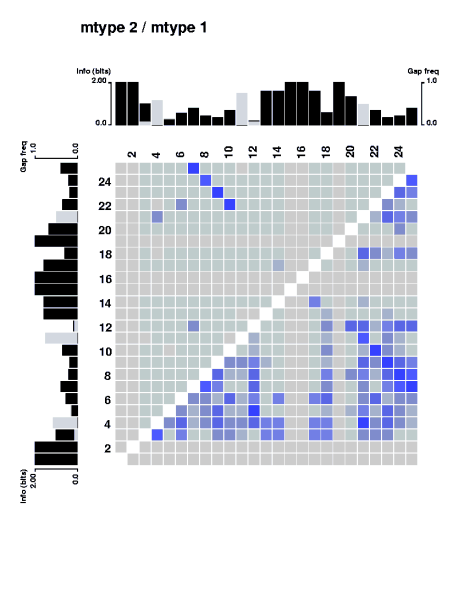
Sample size corrections for plain sequence information content (e.g. Schneider et al. J. Mol. Biol. 188:415-431, 1986; Basharin, Theory Probability Appl. 4:333-336, 1959), and for the standard form of mutual information and correlation functions (e.g. Weiss and Herzel, J. Theor. Biol. 190:341-353, 1998) has previously been studied.
Acknowledgements
Thanks to Anders Krogh for his contribution in the discussion of information content. Thanks to Claus A. Andersen, Lars J. Jensen, and Christopher Workman for suggestions and feedback.
Reference
MatrixPlot: visualizing sequence constraints. J. Gorodkin, H. H. Stærfeldt, O. Lund, and S. Brunak. Bioinformatics. 15:769-770, 1999. (http://www.cbs.dtu.dk/services/MatrixPlot/)